Eigenvalue level repulsion
Imaging we have two matrices ${\bf A}, {\bf B}$ $\in \mathbb{R}^n$, that are both symmetric. Then, we know that both matrices have $n$ eigenvalues (multiplicity). Let’s start now, gradually morphing ${\bf A}$ to ${\bf B}$ using the following formula
$$ {\bf A}[t] = (1 - t) {\bf A} + t {\bf B}, $$
where $t \in [0, 1]$. What will happen is that matrix ${\bf A}$ will have multiple eigenvalues with probability zero, given we have chosen the matrices properly from the set of all real symmetric matrices. In other words, there will be no time $t$ when matrix ${\bf A}$ won’t have $n$ eigenvalues. We can see an example in Figure $1$ below.
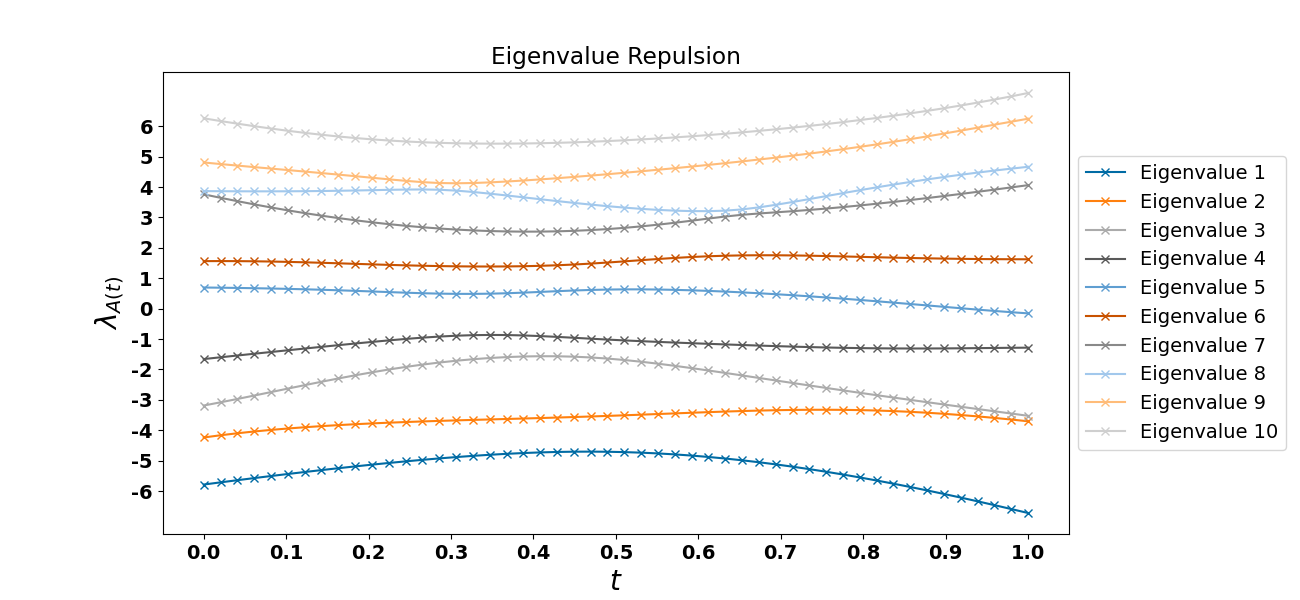
Figure 1. Eigenvalue level repulsion. Notice that as we move from $t=0$ to $t=1$ the eigenvalues of matrix ${\bf A}$ morph to those of ${\bf B}$ and at any instance matrix ${\bf A}$ has $10$ eigenvalues (see the dimension of the matrix ${\bf A}$ in the code snippet below, which is $10$).
The Python code below shows how one can compute the eigenvalue level repulsion.
1import numpy as np
2import matplotlib.pylab as plt
3import matplotlib.style as style
4
5style.use('tableau-colorblind10')
6
7params = {'font.size': 14,
8 }
9plt.rcParams.update(params)
10
11
12def keig(A, k):
13 # Compute the eigenvalues of a matrix, sort them and then choose the k fisrt of them
14 kth_eig = np.sort(np.linalg.eigvals(A))[k]
15 return kth_eig
16
17
18if __name__ == '__main__':
19 np.random.seed(1)
20
21 # Randomly select two matrices A and B and make sure they are symmetric
22 n, nnodes = 10, 50
23 A = np.random.randn(n, n)
24 A = A + A.conj().T
25 B = np.random.randn(n, n)
26 B = B + B.conj().T
27
28 # Define the discretization of interval [0, 1]
29 t = np.linspace(0, 1, nnodes)
30
31 # Run over t and compute the eigenvalues
32 res = []
33 for k in range(n):
34 tmp_mat = []
35 for i in range(nnodes):
36 tmp_mat.append(keig((1 - t[i]) * A + t[i] * B, k))
37 res.append(tmp_mat)
38
39 # Plot the results
40 min_ = int(min(min(res)))
41 max_ = int(max(max(res)))
42
43 fig = plt.figure(figsize=(13, 6))
44 ax = fig.add_subplot(111)
45 for i in range(n):
46 # label numbering should start from 1 not 0
47 ax.plot(t, res[i], '-x', label="Eigenvalue "+str(i+1))
48 ax.set_xlabel(r"$t$", fontsize=20, weight="bold")
49 ax.set_ylabel(r"$\lambda_{A(t)}$", fontsize=20, weight="bold")
50 ax.set_xticks([i/10 for i in range(11)])
51 ticks = ax.get_xticks()
52 ax.set_xticklabels(ticks, fontsize=14, weight='bold')
53 ax.set_yticks([i for i in range(min_, max_)])
54 ticks = ax.get_yticks()
55 ax.set_yticklabels(ticks, fontsize=14, weight='bold')
56
57 pos = ax.get_position()
58 ax.set_position([pos.x0, pos.y0, pos.width * 0.9, pos.height])
59 ax.legend(loc='center right', bbox_to_anchor=(1.25, 0.5))
60
61 ax.set_title("Eigenvalue Repulsion")
62 plt.show()